Pitagóricas
Op2 =OQ2 +PQ2
1=OQ2 +PQ2
Sen(α)= PQ/OP =PQ/1=PQ
1.
2.
3.
Reciprocas
4.
5.
6.
Por cociente
7.
8.
Para demostrar una igualdad podemos:
- Trabajar en los 2 miembros e la igualdad y llegar a un mismo número.
- Obteniendo o llegando a una identidad fundamental.
Ejemplo:
csc(α) * tg(α) = sec (α)
1/sen(α) * sen(α)/cos(α) = sec(α)
1/cos(α) = sec(α)
sec(α) = sec(α)
Ejercicios propuestos
(sec x + tg x) (1- sen x) = cos2 x
cos β * sec β = 1
sen4 β = 1 - cos2 β / csc2 β
sec x / tg x + ctg x = sen x
tg x + cos x / 1+sen x = sec x


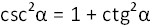






No hay comentarios:
Publicar un comentario